Inleiding
Lewis Carroll hield van spelletjes. Dat komt bijvoorbeeld naar voren in het volgende citaat uit een brief aan May Forshall, één van zijn child-friends[1]:
Speel je wel eens een spel? Of is jouw idee van het leven ‘ontbijt, lessen, diner, lessen, thee, lessen, bed, ontbijt, lessen,’ enzovoorts? Dat is een bijzonder keurig levensplan en bijna net zo interessant als een naaimachine of een koffiemolen.
Hij had altijd een schaakspel bij zich en was een fervent liefhebber van backgammon. In zijn jonge jaren ontdekte hij goochelen en gaf hij vaak voorstellingen voor zijn familie. Hij maakte dankbaar gebruik van het vertekende perspectief dat kenmerkend is voor de goochelaar, om te ontsnappen uit zijn dagelijkse routine [2].
Om zijn broers en zussen te vermaken stelde hij in zijn jonge jaren een reeks tijdschriften samen, elk met meerdere afleveringen. Soms nam hij daarin ook bijdragen van andere familieleden op, maar het meeste schreef hij zelf. De bekendste tijdschriften uit de reeks waren Useful and Instructive Poetry, The Rectory Magazine, The Rectory Umbrella en Mischmasch. Deze bevatten zijn eerste gedichten, parodieën en humoristische vertellingen. Maar we zien er ook diverse ‘raadsel-achtige’ stukjes, zoals bijvoorbeeld het volgende, getiteld ‘Difficulties No. 2’ [3]:
Ik heb twee klokken: de ene loopt in het geheel niet, en de andere loopt een minuut per dag achter: aan welke geef je de voorkeur?
“Degene die achterloopt,” zul je antwoorden, “zonder twijfel.”
Maar let op: degene die een minuut per dag achterloopt, verliest 12 uur, ofwel 720 minuten voordat hij weer de juiste tijd aangeeft, en is daarom slechts eens in de twee jaar correct, terwijl de ander ontegenzeggelijk correct is zo vaak als de tijd die hij aangeeft voorbijkomt, hetgeen twee keer per dag gebeurt.
Als wiskundedocent was hij een liefhebber van ‘recreatieve wiskunde’ en ook in zijn logische werk is vaak een spelelement te herkennen. Dit geldt in het bijzonder voor The Game of Logic waarin hij zijn logica uiteenzet als een spel dat daadwerkelijk door één of meer personen kan worden gespeeld. Hij was gefascineerd door wiskundige en logische puzzels en nam ze ook bijzonder serieus. Hij bedacht zelf ook een groot aantal, waarbij het hem om meer ging dan alleen amusement. Hij hechtte veel waarde aan logisch denken en op deze manier hoopte hij dat te bevorderen.
Spelletjes en puzzels speelden gedurende zijn hele leven een belangrijke rol, alhoewel dit in de beschrijvingen van zijn persoon en werk vaak onderbelicht blijft [4]. Ondanks zijn obsessie met orde en regelmaat, was hij ook gefascineerd door het verstoren van die orde. Dat zien we terug in zijn literaire werk waarin zijn figuren moeten dealen met wanorde en chaos die door anderen gecreëerd is. Vooral in de beide Alice-boeken zet hij zijn lezers voortdurend op het verkeerde been met woordspelingen, dubbelzinnigheden en drogredenen. Volgens Sewell kan het nonsens-element van zijn werk als spel worden beschouwd, meer specifiek als een spel met taal, met wederzijds geaccepteerde regels [5]. Het kan dan ook geen verbazing wekken dat Carroll ook diverse woordspelletjes heeft bedacht.
Het beeld dat hieruit naar voren komt is dat van het prototype van de homo ludens [6]. De term ‘homo ludens’ is afkomstig van Huizinga. Hij karakteriseert de mens als ‘spelend wezen’ en benadrukt de serieuze aard van spel. Volgens Huizinga ligt spel ten grondslag aan vele van onze dagelijkse handelingen en is het een fundament van onze cultuur [7].
In dit artikel geef ik een overzicht van de spelen, raadsels en puzzels die Lewis Carroll heeft bedacht. Ik zal ze eerst naar categorie ordenen en vervolgens aangeven waar ze te vinden zijn. Overigens zijn de overzichten die in de Carrolliaanse literatuur beschikbaar zijn, vaak geordend naar de ‘vindplaats’ of beperkt tot één soort [8].
In mijn overzicht laat ik de volgende problemen, puzzels en raadsels buiten beschouwing:
– degene die zijn opgenomen in zijn literaire, wiskundige en logische boeken;
– degene die geen opgaven zijn, die een competitie-element bevatten of om een
oplossing vragen.
Een indeling in categorieën
Hieronder heb ik de door Carroll bedachte spelen, puzzels en raadsels ingedeeld in de volgende categorieën:
– spelen,
– woordspelletjes en -puzzels,
– wiskundige puzzels en raadsels,
– logische puzzels en raadsels,
– diverse.
Spelen
In de categorie ‘Spelen’ breng ik Carrolls ‘sport-achtige’ spelen, kaartspelen en bordspelen onder.
In Alice’s Adventures in Wonderland komt het croquetspel voor. Carroll ontwikkelde zelf een ingewikkelde variant op het gebruikelijke croquetspel: Croquet Castles. Hij bedacht dit in 1863 terwijl hij met de Liddell-zusjes in de tuin croquet speelde. Een herziene versie heeft hij in 1867 gepubliceerd in Aunt Judy’s Magazine.
Ook is hij de bedenker van een biljartspel: Circular Billiards (1890). Het wordt gespeeld op een ronde tafel met drie biljartballen waarbij één van de ballen de andere achtereenvolgens moet raken.
In zijn jeugd maakte Carroll geen kennis met kaartspelen; het gezin Dodgson deed daar niet aan. Hij leerde zijn eerste kaartspelen pas op 23-jarige leeftijd, maar daarna ontwierp hij er zelf ook enkele:
- Court Circular: een wat eigenaardig spel voor twee of meer spelers, oorspronkelijk bedacht in 1858. Later volgden twee verbeterde versies.
- Ways and Means: een strategisch spel bedacht in 1855, gebaseerd op bieden, kopen en verkopen met gebruik van fiches.
Carroll was ook de geestelijke vader van diverse backgammon-varianten, waarvan de bekendste Co-operative backgammon is. Ook bekend is Lanrick, een spel voor twee spelers op een schaakbord, dat in feite een combinatie is van schaak en backgammon. De eerste vermelding daarvan vinden we in zijn dagboek van 28 december 1878. Er bestaan diverse versies van het spel: sommige gaf hij privé uit en enkele varianten zijn gepubliceerd in The Monthly Packet in 1880 en 1881. De uiteindelijke versie is te vinden in het pamflet Syzegies and Lanrick [9].
Woordspelletjes en -puzzels
Carroll grossierde in woordspelingen, acrostichons, anagrammen e.d. en deze komen (behalve in zijn literaire werken) in ruime mate voor in zijn brieven en dagboeken.
Carroll bekendste en meest succesvolle woordspel is Doublets. Hij bedacht dit tijdens Kerstmis 1877 voor twee meisjes die zich verveelden. Zijn beschrijving is in 1879 door Macmillan uitgegeven. Het spel wordt nog steeds gespeeld, vaak onder de naam Wordladder. Het gaat als volgt. Neem twee woorden met evenveel letters, bijvoorbeeld ‘bord’ en ‘spel’, en probeer ze te verbinden door middel van een opeenvolging van woorden die steeds slechts met één letter van elkaar verschillen, waarbij de volgorde van de letters niet veranderd mag worden. Hoe kleiner het aantal ‘links’ dat je nodig hebt, hoe hoger je score.
Ik werk hieronder een voorbeeld uit (zonder overigens te claimen dat de door mij bedachte oplossing de beste is).
We zoeken de verbinding tussen de woorden ‘bord’ en ‘spel’.
BORD
BOND
ROND
ROOD
ROOK
KOOK
KLOK
BLOK
SLOK
STOK
STEK
STEL
SPEL
Bekend is ook Syzygies, dat Carroll presenteerde in wekelijkse columns in de tijdschriften Vanity Fair en The Lady. Hierboven vermeldde ik al het pamflet waarin het samen met Lanrick is gepubliceerd. Syzygies is afgeleid van Doublets. Ook bij Syzygies gaat het om de verbinding van twee woorden, maar nu kunnen ze van verschillende lengte zijn.
Het gaat als volgt. Pak uit het eerste woord een rijtje met aaneensluitende letters (elk aantal letters is toegestaan); dat noemen we een syzygy. Vind vervolgens een nieuw woord dat dit rijtje letters ook bevat, kies dan een nieuwe syzygy uit dat woord en zoek weer een woord dat dit nieuwe rijtje bevat. Ga hiermee door totdat je het beoogde woord hebt bereikt.
Ik werk weer een voorbeeld uit,. De syzygies staan (zoals bij Carroll zelf) steeds tussen haakjes. We gaan van ‘tandarts’ naar ‘code’.
TANDARTS
(dar)
endeldarm
(ende)
genderneutraal
(aal)
codetaal
(code)
CODE
Uiteraard had Carroll hierbij ook een puntentelling. In zijn oorspronkelijke versie hanteerde hij hiervoor de volgende methode. De score is het aantal letters in de langste syzygy (4 in ons geval) plus 7 keer het aantal letters in de kortste syzygy (7 x 3 = 21), minus het aantal “waste letters” (het aantal letters dat in geen enkele syzygy voorkomt (15) en minus het aantal link-woorden (3). Dus de score is 4 + 21 – 15 – 3 = 7.
Toelichting: “waste letters” zijn letters die niet voorkomen in de syzegy boven of onder het betreffende woord: dus in ’endeldarm’ zijn de ‘l’ en de ‘m’ waste letters.
Ik weet niet of mijn verbinding tussen ‘tandarts’ en ‘code’ degene met de hoogste score is; het is in ieder geval niet de snelste. Want je kunt natuurlijk heel snel de verbinding maken door bij maar één letter als syzygy te kiezen:
TANDARTS
(d)
CODE
Maar in dat geval is de score wel bijzonder laag, namelijk 1 + 7 – 9 – 1 = -2.
Ten slotte noem ik hier nog Mischmasch, een woordspel voor twee spelers dat Carroll bedacht in 1882 (niet te verwarren met het tijdschrift uit zijn jeugd met dezelfde naam). De ene speler noemt drie of vier letters en de andere speler moet raden van welk woord ze deel uitmaken.
Wiskundige puzzels en raadsels [10]
Als wiskundige én liefhebber van puzzels had Lewis Carroll zijn hele leven een grote belangstelling voor ‘recreatieve wiskunde’ (wiskunde als vermaak). Het ging hem daarbij niet alleen om creaties van anderen, hij bedacht zelf ook vele bijzondere problemen, opgaven, puzzels en raadsels.
Waarschijnlijkheidsraadsels
Binnen de wiskundige puzzels had hij een speciale voorliefde voor problemen op het gebied van waarschijnlijkheid. In zijn bundeling uit 1893 van wiskundige puzzels onder de titel Pillow Problems gaan 13 van de 72 opgaven over waarschijnlijkheid. Als voorbeeld geef ik hier Question 5: Een zak bevat één fiche dat ofwel wit ofwel zwart is. Er wordt een wit fiche in de zak gestopt, de zak wordt geschud en vervolgens wordt er een fiche uit genomen, dat wit blijkt te zijn. Hoe groot is daarna de kans om een wit fiche uit de zak te halen? [11]
Geometrische raadsels
Een voorbeeld van zijn geometrische raadsels is de paradox, die na zijn dood is aangetroffen in zijn aantekeningen.
Teken een rooster met 8 x 8 = 64 vierkantjes en knip het in vier stukken, zoals is aangegeven in figuur 1. Wanneer we de vier stukken herschikken krijgen we een rooster met 5 x 13 = 65 vierkantjes. Hoe komen we aan dat extra vierkantje?
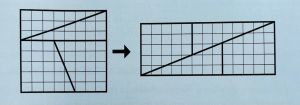
figuur 1
Een ander voorbeeld is het vier kleurenprobleem. Dat was in Carrolls tijd een bekend raadsel en hij maakte er een spel voor twee personen van. Het oorspronkelijke probleem bestond uit de volgende vraag: kan iedere landkaart met slechts vier kleuren worden gekleurd wanneer gebieden die aan elkaar grenzen, verschillende kleuren moeten hebben (zie figuur 2)?
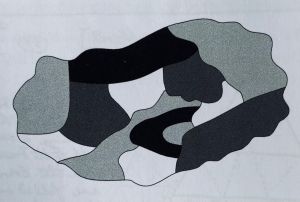
figuur 2
De variant van Lewis Carroll gaat als volgt. Laat persoon A een denkbeeldige kaart tekenen, verdeeld in een aantal gebieden. Persoon B moet de gebieden kleuren met een zo klein mogelijk aantal kleuren, waarbij twee aan elkaar grenzende gebieden verschillende kleuren hebben. Hierbij wordt A uitgedaagd om de kaart zodanig te tekenen dat B zoveel mogelijk kleuren moet gebruiken.
De hierboven al aangehaalde bundel Pillow Problems bevat veel geometrische puzzels.
Rekenkundige raadsels
Een aantal van Carrolls rekenkundige raadsels is gebundeld in A Tangled Tale (uit 1885), waaronder de volgende.
Twee reizigers wandelen van 15 uur tot 17 uur een heuvel op en terug: Gemiddeld lopen ze een tempo van 4 mijl per uur, heuvel op 3 mijl per uur, heuvel af 6 mijl per uur. Bepaal de afstand die ze hebben afgelegd en het tijdstip waarop ze de top van de heuvel bereiken (op een half uur nauwkeurig)[12].
Ook voor diverse tijdschriften bedacht hij rekenkundige puzzels, waaronder The Monthly Packet. Hier volgt als voorbeeld Cats and rats (februari 1880).
Als 6 katten 6 ratten doden in 6 minuten, hoeveel katten zijn er dan nodig om 100 ratten te doden in 50 minuten?
In een latere aflevering gaf hij het probleem Cats and rats again: Als een kat een rat kan doden in één minuut, hoelang duurt dan het doden van 60.000 ratten? Hij voegde hieraan toe dat naar zijn mening de ratten de kat zouden doden.
Getallen raden
Op latere leeftijd raakte Carroll geïnteresseerd in problemen waarbij een getal moest worden geraden: een persoon neemt een getal in gedachten en na een reeks vragen en berekeningen kan dit getal worden gereconstrueerd. Ook maakte hij indruk in gezelschap met opteltrucs. Een daarvan ging als volgt. Carroll schreef een willekeurig getal van vijf cijfers op. Iemand anders zette daar een willekeurig getal van vijf cijfers onder. Dan schreef Carroll een derde getal, de ander een vierde. Carroll voegde een vijfde getal toe, waarna hij onmiddellijk de som van de vijf getallen kon geven[13] .
Logische puzzels en raadsels
Carroll hechtte veel waarde aan logica en vond het belangrijk dat iedereen logisch leerde denken en redeneren. Zijn eerste logische werk, The Game of Logic, presenteerde hij ook in de vorm van een spel, om de toegankelijkheid ervan te vergroten. Ook veel voorbeelden in zijn logisch hoofdwerk, Symbolic Logic, zijn speels. Deze blijven hier buiten beschouwing. Daarnaast bedacht hij ook veel logische raadsels, zowel als amusement als vanwege het educatief aspect. In diverse van zijn raadsels speelt het verschijnsel ‘tijd’ een hoofdrol. Dat begon al op jonge leeftijd, gelet op een tweetal voorbeelden uit The Rectory Umbrella (Difficulties No. 1 en No. 2). No. 2 (The Two Clocks) beschreef ik al in de inleiding. No 1, Where does the day begin, gaat als volgt.
Altijd is zo ongeveer de helft van de wereld in zonlicht en omdat de wereld ronddraait verschuift dit achtereenvolgens over verschillende delen van de wereld. Stel het is dinsdag en in Londen begint de ochtend. Een uur later zal het dinsdagmorgen zijn in het westen van Engeland. Als de hele wereld uit land bestond, zouden we de dinsdagmorgen de hele wereld rond kunnen volgen gedurende 24 uur, totdat we weer in Londen zijn. Maar we weten dat het in Londen dan 24 uur later is en dat het niet dinsdagmorgen maar woensdagmorgen is. Waar in de rondgang over de aarde, verandert de dag van naam?
Bekend is ook The monkey and the weight problem. Soms wordt ernaar verwezen als Lewis Carroll’s monkey puzzle (zie figuur 3) maar het is onzeker of Carroll dit raadsel zelf heeft bedacht[14].
Een gewichtloos en volledig flexibel touw hangt over een gewichts- en weerstandsloze katrol, die vastzit aan het dak van een gebouw. Aan het ene eind van het touw hangt een gewicht dat precies in evenwicht is met een aap aan het andere eind. Nu begint de aap te klimmen: wat gebeurt er met het gewicht?

figuur 3
Ook heeft Carroll diverse varianten bedacht van River crossing puzzles, een bekend puzzelthema dat terug schijnt te gaan tot de 9e eeuw. Een voorbeeld[15]. Vier mannen en hun echtgenotes willen de rivier oversteken met een boot die niet meer dan twee personen tegelijk kan vervoeren. Geen van de beide mannen mag zijn vrouw aan de oever achterlaten tenzij ze alleen is of slechts in vrouwelijk gezelschap. Hoe krijgen ze dat voor elkaar?
Bijzonder bekend zijn de paradoxen die Carroll publiceerde in Mind: The Barbershop Paradox en What the Tortoise Said to Achilles. Deze beschreef ik eerder in Phlizz al uitgebreid[16]. Daarnaast bedacht hij een aantal varianten op de paradox van de leugenaar, die overigens lang niet altijd als raadsel of puzzel waren geformuleerd. Elders beschreef ik al eens de bekende variant Crocodillus[17]. Het volgende probleem met betrekking tot ‘liegen’ is wel duidelijk een raadsel:
A zegt dat B liegt.
B zegt dat C liegt.
C zegt dat A en B liegen.
Wie liegt en wie spreekt de waarheid?[18]
Diverse
Carrolls dagboeken bevatten een variëteit aan bijzondere spelletjes en raadsels die niet passen in de bovenstaande indeling. Gardner [1996] geeft het volgende overzicht:
- Origami, met onder andere aanwijzingen hoe je een handdoek als muis of konijn kunt vouwen.
- Mnemonics: hoe cijfers om te zetten in gemakkelijk te onthouden woorden.
- Ciphers: codes voor een geheimschrift.
- Spelletjes en puzzels in de vorm van tekeningen, met name voor kinderen.
Tot slot volgen hier nog twee korte raadseltjes, afkomstig uit zijn brieven[19]:
Why is Agnes like a thermometer?
Because she won’t rise when it’s cold.
Why is a pig that has lost its tail like a little girl on a seashore?
Because it says “I should like another tale, please!”
De vindplaatsen
Hieronder geef ik een overzicht van de verschillende vormen waarin Carroll zijn puzzels genoteerd en verspreid heeft. Tot slot zal ik nog ingaan op bundelingen die na zijn dood tot stand zijn gebracht.
Carrolls ‘publicatiebeleid’
Spelletjes en puzzels van Lewis Carroll zijn overal te vinden: in zijn dagboeken, brieven, pamfletten, logische en wiskundige werken en literaire werk. Toch had Carroll wel degelijk nagedacht hoe hij dit alles systematisch zou kunnen ontsluiten voor een groter publiek.
Zijn oudste raadsels vinden we in The Rectory Umbrella, dat uitkwam in de jaren 1850-1853. Dit betreft met name de al vermelde Difficulties No. 1 en No. 2.
Een aantal spelen en puzzels bracht hij zelf uit in pamfletten. Dat betreft:
1860: het kaartspel Court Circular.
1863: de croquet-variant Croquet Castles: For Five Players.
1879: het bordspel Lanrick: A Game for Two Players.
1882: het woordspel Mischmasch: A Word-Game For Two Players Or Two Sets of Players.
1893: de combinatie Syzygies and Lanrick.
Hij bracht ook enkele afzonderlijke publicaties uit bij uitgever Macmillan:
- Doublets, a word-puzzle (1879).
Dit bevat het hierboven beschreven spel Doublets: de regels, de puntentelling, een woordenlijst van “all well-known English words […] of 3, 4, 5, or 6 letters, which may be used in good Society and which can serve as Links” [20]. En het bevat de doublets die hij heeft gepubliceerd in het tijdschrift Vanity Fair inclusief hun oplossing. - A Tangled Tale (1885).
Van april 1880 tot november 1884 schreef Carroll een puzzel-column voor het tijdschrift The Monthly Packet. In elk nummer stond een verhaal dat een wiskundig probleem bevatte. Het boekje geeft een overzicht van deze tien verhalen die hij ‘Knots’ noemde, met illustraties van Arthur B. Frost. Maar het bevat ook de reacties van de lezers met mogelijke oplossingen die hij ontving, voorzien van zijn commentaar en de juiste oplossing. - Pillow Problems thought out during wakeful hours (1893).
Dit is uitgegeven als deel II van Curiosa Mathematica (deel I was A new theory of parallels.) De 72 daarin opgenomen, vaak ingenieuze, problemen beslaan diverse terreinen van de wiskunde: rekenkunde, meetkunde, trigonometrie, differentiaalrekening en waarschijnlijkheidsleer.
Al enkele malen kwam aan de orde dat hij ook voor tijdschriften raadsels en puzzels schreef. Hieronder geef ik een overzicht van de betreffende tijdschriften.
- Vanity Fair publiceerde in de periode 1879-1881 doublets, waar de lezers op konden reageren.
- In The Lady verschenen in 1891 en 1892 Syzegies, gecombineerd met een wekelijkse dialoog met het publiek. Uit de aantallen reacties wordt duidelijk dat Doublets als spel populairder was dan Syzegies.
- The Monthly Packet (een christelijk tijdschrift voor jonge meisjes) presenteerde in de periode april 1880 – november 1884 verhalen van Carroll die een wiskundig probleem bevatten. Deze heeft hij later uitgegeven onder de titel A Tangled Tale.
- In The Monthly Packet verscheen ook Mischmasch (in 1881) dat hij later, in 1882, als eigen pamflet uitgaf.
- Voor Aunt Judy’s Magazine (december 1870) maakte hij zeven puzzels onder de titel ‘Puzzles from Wonderland’; het betrof vooral woordpuzzels.
- In The Educational Times werden vanaf 1879 tien van zijn wiskundige problemen gepubliceerd, inclusief oplossingen, waarvan één posthuum.
Ten slotte bevatten Carrolls dagboeken en brieven een grote variatie aan puzzels, woordspelletjes, paradoxen, grappen, anagrammen, coderingsmethoden, opteltrucs, origami e.d. In zijn nalatenschap zijn ook veel aantekeningen met spelletjes puzzels en raadsels gevonden[21]. De puzzels in de correspondentie bevatten zelden een oplossing.
Enkele jaren geleden is een aantal handgeschreven puzzels ontdekt die Carroll vanaf 1853 had gedeeld met zijn wiskunde-mentor Barthlomew Price, het zgn. Dodgson/Price Archive. Het bevat reeds bekende puzzels, zowel van Carroll zelf als van anderen (zoals The Monkey and the weight puzzle), maar ook tot dan toe onbekende puzzels.
‘Original Games and Puzzles’
Carroll had enkele publicaties in voorbereiding die hij uiteindelijk niet voltooide. Uit zijn dagboek (17 september 1878) weten we dat hij een puzzelboek aan het maken was voor de familie Hull. Ook voor de kinderen van Robert Gascoyne-Cecil wilde hij een dergelijke bundeling samenstellen. Maar hij werkte ook jarenlang aan een omvangrijk ‘puzzelboek’ dat bedoeld was als deel III van Curiosa Mathematica. Oorspronkelijk had hij hiervoor hij de titel Alice’s Puzzle Book in gedachten, maar later veranderde hij die in Original Games and Puzzles[22].
In zijn dagboekaantekening voor 1 maart 1875 lezen we dat het idee voor dit puzzelboek bij hem ontstond op 8 januari 1875; kort daarna stemde Macmillan ermee in om een voorplaat te ontwerpen. In 1881 noemde Carroll het opnieuw, nu met een door Miss Thomson ontworpen voorplaat, evenals in 1885. In The Lady van 11 februari 1892 maakte hij melding van een “some-day-to-be-published book of Games and Puzzles” en ook in de inleiding van Sylvie & Bruno Concluded (1893) kondigde hij aan dat een werk getiteld Original Games and Puzzles in voorbereiding was. Maar het is er uiteindelijk niet meer van gekomen.
Carrolls neef Stuart Dodgson Collingwood die de eerste biografie over Carroll schreef, verklaarde dat hij in de nalatenschap geen voorbereidende stukken voor het boek had kunnen vinden. In The Lewis Carroll Picture Book (1899) nam Collingwood wel een aantal afzonderlijk gepubliceerde puzzels op waarvan hij dacht dat Carroll ze in zijn puzzelboek had willen opnemen.
Hoe dan ook, Carroll was ver met zijn voorbereiding voor Original Games and Puzzles. Volgens Crutch [1981] zou het in ieder geval de volgende onderdelen bevatten:
- De ook apart gepubliceerde Croquet Castles, Doublets, Syzegies en Lanrick.
- Enkele andere aparte publicaties die inmiddels out-of-print waren zoals Court Circular, Circular Billiards, Mischmasch.
- Bijdragen aan tijdschriften: Puzzles in Wonderland, verschenen in Aunt Judy’s Magazine, en Co-operative Backgammon, gepubliceerd in The Educational Times.
- Niet gepubliceerd materiaal dat niet voor specifieke personen bestemd was, zoals Anagrammatic Sonnet, Memoria Technica en de Telegraph Cipher, ook al waren dat strikt genomen geen spelletjes.
Het was niet zijn bedoeling om de al gepubliceerde Pillow Problems, A Tangled Tale and Game of Logic op te nemen. Ook logische problemen zoals opgenomen in Symbolic Logic zouden achterwege blijven, evenals stukken over het schaakspel. Puzzels en acrostichons uit brieven die bedoeld waren voor specifieke vrienden, wilde hij ook niet opnemen.
Mogelijke kandidaten waren volgens Crutch wel het raadsel A monument all men agree uit zijn eigen tijdschrift Mischmasch, het probleem Cats and Rats dat eerder was uitgebracht in The Monthly Packet en twee manuscripten, Arithmetical Croquet en Number-Guessing. Crutch noemt ook twijfelgevallen: enkele tekeningen, de twee Difficulties uit The Rectory Umbrella, The Monkey and the Weight Problem en The Postal Problem (over een dubbelzinnigheid in de Post Office Guide).
En verder ….
Na Carrolls dood zijn diverse bundelingen van zijn raadsels en puzzels uitgebracht, vaak voorzien van een oplossing die Carroll er zelf – zeker in zijn brieven – niet altijd bij gegeven had.
De eerste bundeling is te vinden in het al genoemde The Lewis Carroll Picture Book van de neef Stuart Dodgson Collingwood (1899).
In 1979 verscheen een verzameling, bijeengebracht door Edgar Cuthwellis, Lewis Carroll’s Bedside Book (London: Dent). Deze is in het Nederlands vertaald door Willem Wilmink: Wakker Liggen (Utrecht: Bruna, 1980).
Edward Wakeling heeft een aantal bundelingen van puzzels uitgebracht, voorzien van een toelichting en oplossingen:
Lewis Carroll’s Games & Puzzles (New York: Dover 1992).
Rediscovered Lewis Carroll Puzzles (New York: Dover 1995).
‘Recreational Mathematics’ in Wilson & Moktefi (eds.) 2019.
Een combinatie van Carrolls puzzels en aantal door Wakeling zelf bedachte puzzels is te vinden in Alice in Wonderland Puzzle and Gamebook (Cove Press, 1995).
Overzichten met toelichting zijn ook te vinden in:
John Fisher, The Magic of Lewis Carroll (London: Nelson, 1973).
Martin Gardner, The Universe in a Handkerchief. Lewis Carroll’s Mathematical Recreations, Games, Puzzles, and Word Plays (New York: Copernicus, 1996).
Carrolls recreatieve wiskunde komt aan de orde in:
Marcel Danesi, Blending Logic and Imagination. The Puzzle Art of Lewis Carroll (New York: Nova Scientific Publishers, 2020).
Robin Wilson, Lewis Carroll in Numberland. His Fantastical Mathematical Logical Life, London: Allen Lane, 2008, met name pp.149-171).
In het recent verschenen Lewis Carroll’s Cats and Rats … and Other Puzzles with Interesting Tails van Yossi Elran (World Scientific, 2021) wordt een aantal wiskundige puzzels met bijzondere aspecten beschreven en geanalyseerd. Eén daarvan is het al genoemde Cats and Rats, met als bijzonderheid dat deze puzzel meerdere oplossingen heeft omdat een deel van de informatie die nodig is voor een eenduidige oplossing, ontbreekt[23].
Veel aandacht voor Carrolls logische puzzels is te vinden in: Jason Rosenhouse, Games for Your Mind. The History and Future of Logic Puzzles (Princeton University Press 2020).
Carrolls werken inspireerden ook diverse bedenkers van puzzels tot nieuwe problemen en varianten, waarbij men Lewis Carroll noemt als inspiratiebron en soms ook een relatie legt met zijn literaire werk. Vermeldenswaard is zeker Raymond M. Smullyan (1919-2017) die wel “a modern day Lewis Carroll” is genoemd, een Amerikaans wiskundige, logicus en filosoof maar ook een pianist en illusionist. In Alice in Puzzle-land, A Carrollian Tale for Children Under Eighty (New York: Dover, 1982) heeft hij een groot aantal puzzels verwerkt in een verhaal. Ook het hoofdstuk ‘Alice in the Forest of Forgetfulness’ in What is the Name of This Book? bevat Carroll-gerelateerde raadsels (New York: Dover, 1978).
Ten slotte trof ik nieuwe, op Carroll en de Alice-boeken geïnspireerde puzzelverzamelingen aan in:
- Martin Gardner, The Snark Puzzle Book (New York: Prometheus Books, 1990).
- Richard Wolfrik Galland, Lewis Carroll’s Puzzles in Wonderland (London: Carlton Books, 2013).
- Jason Ward, Alice’s Puzzles Through the Looking Glass (London: Carlton Books, 2016).
- Gareth More, Alice’s Puzzle Adventures in Wonderland (London: Carlton Kids, 2019).
- Lilac Mohr, Math & Magic in Wonderland (2016), waarin de puzzels in een verhaal zijn verwerkt.
Dit overzicht heeft echter geenszins de pretentie volledig te zijn.
Conclusie
Ik heb geprobeerd een indruk te geven van de spelen, spelletjes, puzzels en raadsels die Lewis Carroll heeft bedacht buiten zijn literaire, wiskundige en logische werken. Hij herhaalde zelden een puzzel en mede daardoor bereikte hij een geweldige productie. Vermoedelijk is er zelfs nog meer dan we nu weten, want er wordt nog steeds nieuw materiaal ontdekt, bijvoorbeeld in zijn brieven die door anderen ontvangen en bewaard zijn. Onlangs kwam nog een raadsel boven water in de geschreven herinneringen van child-friend Mabel Burton, die samen met Carrolls brieven aan haar bewaard waren gebleven[24].
Het is niet eenvoudig deze productie overzichtelijk in kaart te brengen. De ordening die Carroll zelf wilde aanbrengen in Original Games and Puzzles is uiteindelijk niet gerealiseerd, vermoedelijk omdat hij al een veelheid van projecten om handen had in de laatste jaren van zijn leven.
In zijn puzzels en raadsels herkennen we het spelelement dat de meesten vooral kennen uit zijn literaire werk. Uit zijn brieven en dagboeken wordt duidelijk dat dit spelelement ook een belangrijke rol had in zijn omgang met zowel volwassenen als kinderen. De hoeveelheid en de breedte van de spreiding versterken het beeld van Carrolls veelzijdigheid en leveren een waardevolle bijdrage aan het inzicht in zijn boeiende persoonlijkheid.
Voetnoten
[1] Geciteerd in Blake 1974, p.11. Vertaling Bas Savenije.
[2] Fischer 1973, p.9
[3] Uit The Rectory Umbrella [Carroll 1932, p.78]. Vertaling Bas Savenije.
[4] Guiliano 2019, p.142.
[5] Sewell 1952.
[6}Zie bijvoorbeeld Peeters 2013, p.136 en Blake 1974, p.104 (”Carroll’s art expresses a kind of game player’s mentality”).
[7] Huizinga 1952.
[8] Zie bijvoorbeeld resp. Gardner 1969 en Wakeling 2019.
[9] De eerste editie van Syzegies and Lanrick is uit 1893 en de tweede uit 1893, zie ook Wakeling 1992. De Lanrick-versies uit 1879 en 1880 zijn te vinden in Jabberwocky – The Journal of the Lewis Carroll Society, Vol. 11, No. 1, Winter 1981/82.
[10] Deze paragraaf is in belangrijke mate gebaseerd op Wakeling 2019.
[11] De oplossing: 2/3.
[12] De oplossing: 24 mijl, 18.30 uur.
[13] Overgenomen uit Gardner 1996, p. 43.
[14] Overgenomen uit Wakeling 2019, p.153; oorspronkelijk afkomstig uit Sam Loyd’s Cyclopedia of Puzzles.
[15] Overgenomen uit Wakeling 1995, p.17.
[16] Phlizz d.d. september en december 2020, zie ook Savenije 2021, hoofdstuk 7 en 8.
[17] Phlizz d.d. september 2020, zie ook Savenije 2021, p.76.
[18] Overgenomen uit Gardner 1996, p.22. Oplossing: B spreekt de waarheid.
[19] Raadsels overgenomen uit Gardner 1996, p.49.
[20] Carroll 1879, p.10.
[21] Zie Gardner 1996.
[22] In Crutch 1981 en Morgan 2015 vinden we een reconstructie van de geschiedenis en inhoud van dit puzzelboek.
[23 Het gaat hierbij met name om “the cats’ working procedure”: Werken de katten alleen of in groepen? En, als ze in groepen werken, wat is dan de groepsgrootte?
[24] Zie Wakeling 2019, p.175.
Literatuur
Blake, Kathleen, 1974, Play, Games, and Sport. The Literary Works of Lewis Carroll, Ithaca: Cornell University Press.
Carroll, Lewis, 1879, Doublets. A Word-Puzzle, London: Macmillan
Carroll, Lewis, 1885, A Tangled Tale, London: Macmillan.
Carroll, Lewis, 1893, Pillow Problems, London: Macmillan.
Carroll, Lewis, 1932, The Rectory Umbrella and Mischmasch, London: Cassell & Co.
Collingwood, Stuart Dodgson, 1899, The Lewis Carroll Picture Book, London: Fisher Unwin.
Crutch, Denis, 1981, ‘Lewis Carroll’s Original Games and Puzzles’, Jabberwocky, Vol. 11, No. 1, pp.3-6.
Danesi, Marcel, 2020, Blending Logic and Imagination. The Puzzle Art of Lewis Carroll, New York: Nova Scientific Publishers.
Fisher, John (ed.), 1973, The Magic of Lewis Carroll, London: Nelson.
Gardner, Martin, 1996, The Universe in a Handkerchief. Lewis Carroll’s Mathematical Recreations, Games, Puzzles, and Word Plays, New York: Copernicus.
Guiliano, Edward, 2019, Lewis Carroll: The World of His Alices, Brighton: Edward Everett Root Publishers.
Huizinga, J., 1938, Homo Ludens. Proeve eener bepaling van het spel-element der cultuur, Haarlem: Tjeenk Willink & Zoon.
Morgan, Christopher (ed.), 2015, The Pamphlets of Lewis Carroll: Volume 5, Games, Puzzles, & Related Pieces, Lewis Carroll Society of North America.
Peeters, Carel, 2013, Het wonderland van Lewis Carroll, Amsterdam: Uitgeverij De Harmonie.
Rosenhouse, Jason, 2020, Games for Your Mind. The History and Future of Logic Puzzles, Princeton University Press.
Savenije, Bas, 2021, De logische wereld van Lewis Carroll en wat Alice daar aantrof, Lewis Carroll Genootschap.
Sewell, Elisabeth, 1952, The Field of Nonsense, London: Chatto & Windus.
Wakeling, Edward, 1992, Lewis Carroll’s Games & Puzzles, New York: Dover Publications.
Wakeling, Edward, 1995, Rediscovered Lewis Carroll Puzzles, New York: Dover Publications.
Wakeling, Edward, 2019, ‘Recreational Mathematics’, in Wilson & Moktefi (eds.) 2019, pp.141-176.
Wilson, Robin & Amirouche Moktefi, 2019, The Mathematical World of Charles L. Dodgson (Lewis Carroll), Oxford University Press.
[print_button]


