DIVERSE WISKUNDIGE “ALICE”- WAARNEMINGEN
Paradox
De Caucus[1]-race in hoofdstuk 3 van Wonderland kun je zien als voorbeeld voor de bekende paradox van Achilles en de schildpad, opgesteld door de Griekse filosoof Zeno (ca. 490 v.Chr. – ca. 430 v.Chr.). Hierin “bewijst” Zeno dat Achilles (de snelste loper uit die tijd) nooit een schildpad, die een voorsprong heeft gekregen, zou kunnen inhalen. Zeno’s argument is gebaseerd op het feit dat je afstand oneindig kunt blijven delen. Helaas heb je ook nog met een factor tijd te maken. Maar om deze paradox mathematisch op te lossen moest eerst het onderdeel calculus met het limietbegrip binnen de wiskunde ontwikkeld worden met daarin het bewijs dat de som van een oneindig aantal stappen toch eindig is. Dodgson heeft andere paradoxen ontwikkeld waarvan de bekendste was ”Wat de schildpad zei tegen Achilles”[2], (de omgekeerde paradox van Achilles en de schildpad) die onder andere door Bertrand Russell en vele andere filosofen becommentarieerd is geweest en het centrale thema is in het opmerkelijke boek van Douglas Hofstadter: Gödel, Escher, Bach uit 1979 met als ondertitel een metaforische fuga (muziekvorm) op mensen en machines in de geest van Lewis Carroll.
Deze caucus race heeft helemaal geen regels en geen afgesproken begin of einde. Iedereen rent of rent niet en aan het einde, als de Dodo plotseling uitroept dat de race voorbij is, heeft iedereen gewonnen.

A Mad Tea-Party
Je zou de titel van het zevende hoofdstuk uit Wonderland ook kunnen lezen als een M. T. (em(p)ty) party, een lege (politieke) partij die alleen maar loze beloften doet. Merk op dat het Engelse woordje tea wordt uitgesproken als de Engelse letter t en deze t staat natuurkundig voor het belangrijke woordje tijd in dit hoofdstuk.
Op het prijskaartje van de hoed van de Hoedenmaker staat “In this style: 10/6”. Dat moet natuurlijk gelezen worden als 10 shilling en 6 pence in de Engelse muntsoort. Uitgaande van 1 shilling is 12 pence, kom je in totaal uit op 126 pence en dat is (opmerkelijk) weer 3 (oorspronkelijk 3 figuren aan de tafel) x 42. Maar is dit wel een prijskaartje?
We kunnen dit kaartje ook wiskundig lezen als “In this style: 106”, waarbij 106 = 1.000.000. Wellicht een beetje vreemd dat de Hoedenmaker 1 miljoen hoeden in deze stijl heeft geproduceerd. Maar laten we verder kijken. We delen deze 1 miljoen door 7 (de leeftijd van Alice in Wonderland) en krijgen dan 142857 met rest 1. En kijk dan eens naar de volgende tabel, die Carroll kende en ook vaak gebruikte:
106 : 7 = 142857 met rest 1; 1/7 = 0,142857…
142857 x 2 = 285714; 2/7 = 0,285714…
142857 x 3 = 428571; 3/7 = 0,428571…
142857 x 4 = 571428; 4/7 = 0,571428…
142857 x 5 = 714285; 5/7 = 0,714285…
142857 x 6 = 857142; 6/7 = 0,857142…
142857 x 7 = 999999
De cijfers in de producten en delingen vormen een cyclische verwisseling van de 6 cijfers van 142857. Verder worden de 6 cijfers in de breuken cyclisch herhaald. Welke betekenis schuilt hier dan achter?
Als later de Hoedenmaker als getuige bij de rechtsspraak wordt opgeroepen en beschuldigd wordt van M(urdering) T(ime) (weer em(p)ty!!!) blijft hij nerveus heen en weer hippen op zijn voeten als in een periodieke (cyclische) beweging. De klacht van de Hoedenmaker is dat hij vast in de tijd zit, de eeuwigdurende thee-tijd om 6 uur. De tijd staat stil en dus moeten de gasten aan tafel in beweging komen. Dat komt omdat de waarde van zijn hoed niet precies matcht met 1 miljoen. Om bij 999999 uit te komen moet hij de som 1.000.000 – 1 maken en dat lukt klaarblijkelijk alleen als hij in alle verwarring een hap uit zijn theekopje neemt. Op datzelfde moment begint Alice exponentioneel te groeien. We stappen nu van een lineair getallensysteem over naar een modulair getallensysteem. (Als voorbeeld bij dit laatste: tijdsaanduiding bij een klok, na 12 wordt opnieuw bij 1 begonnen).
Lees nu eens de tekst op de hoed (In this style 10/6) als In this mode 106.[3] Deel 106 door 7 en je houdt als rest 1 over.
Iets formeler gezegd: 106 ≡ 1 (mod 7) (vertaald: 106 en 1 zijn congruent modulo 7; 106 en 1 hebben na deling door 7 dezelfde rest) oftewel
107-1 ≡ 1 (mod 7) en zie daar verschijnt de kleine stelling van Fermat[4]:
ap-1 ≡ 1 (mod p) met p een priemgetal en a en p onderling niet deelbaar[5]
We kunnen het prijskaartje op de hoed dus zien als een manier om eerbetoon te brengen aan Pierre de Fermat. De titel van dit hoofdstuk A Mad Tea Party is nu te herleiden tot:
A Mod(ular) T(ime) Parti(-cle)
(Een modulair tijdsdeeltje)

Schoppen en Harten
Uit hoofdstuk 8 in Wonderland komt de scène voor met de drie schoppenkaarten. De schoppenkaarten zijn de tuinlieden in Wonderland en zijn doodsbang voor de Hartenkoningin, die ze beschouwen als een blinde en doelloze wraakgodin en waarschijnlijk een irrationaal[6] getal representeert.

Haar enthousiasme om iedereen te executeren komt vanwege een afgrijselijke woordspeling met het woord “axes”, het meervoud van een axis (x-as en y-as) bij een grafiek.

De vraag bij deze conversatie is natuurlijk waarom juist schoppen 2, 5 en 7 worden opgevoerd. Het simpele antwoord is natuurlijk vanwege het feit dat de som van de getallen op de drie kaarten 2 + 5 + 7 = 14 en vermenigvuldigd met 3 (aantal kaarten) dit weer 42 oplevert. Maar er zit een diepere laag onder. Als je 7 deelt door 5, krijg je een benadering van het irrationale getal wortel 2 (in 1 decimaal nauwkeurig). Dus 7 : 5 = √2 ≈ 1,4142. Het Engelse woord root in tulips-roots verwijst dus naar het symbolische woord wortel dat in de wiskunde wordt gebruikt.[7]
De oudste regel in het boek van de Hartenkoning is regel 42[8]. Waarop Alice opmerkt dat de oudste regel natuurlijk regel 1 moet zijn. Een verwijzing naar het feit dat zij het leiderschap van Hartenkoning en Hartenkoningin zo dadelijk gaat overnemen? Dat stond natuurlijk al bij voorbaat vast, want haar naam Alice bevat het woordje ace.
Hetzelfde geldt overigens ook met betrekking tot Spiegelland, waar Alice aan het eind van het boek tot koningin wordt gepromoveerd. Ongeacht alle capriolen die Alice moest uithalen, wist ze van tevoren al dat dat de onbekende Schaakgrootmeester haar had voorbestemd als dé nummer 1, dus als koningin te laten eindigen.
Humpty-Dumpty

De filosoof Humpty-Dumpty is voornamelijk geschoold in linguïstische zaken. Wellicht suggereert Carroll in het fragment links dat filosofen, volop in het toenmalige Oxford aanwezig, over het algemeen nauwelijks begiftigd zijn met enige wiskundige kennis.

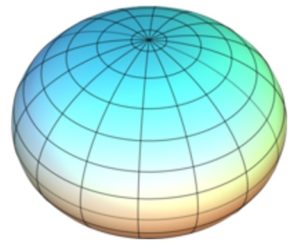
Het voorkomen van Humpty-Dumpty is wiskundig bezien een oblate (afgeplatte) sferoïde (een omwentelingslichaam van een ellips). De aarde wordt ook vaak als een oblate sferoïde voorgesteld.
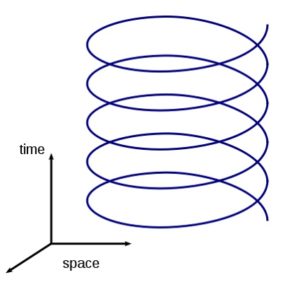
De helix of schroeflijn in de vorm van een kurketrekker komt bij Carroll in Spiegelland regelmatig voor. Humpty-Dumpty vergelijkt bijvoorbeeld de “toves” met kurketrekkers en ook John Tenniel tekende bijvoorbeeld de geit en de eenhoorn met spiraalvormige hoorns. Een helix is een 3-dimesionale kromme met constante straal en spoed. De helix is een speciale vorm van een spiraal.[9]
Speltheorie

In hoofdstuk 9 van Wonderland komt in de dialoog van Alice met de Hertogin voor de zevende keer in het begin van dit hoofdstuk het woordje moraal langs. Dit keer met de woorden meer en minder. Dit is duidelijk een voorbeeld van een nulsomspel. Dit is in de speltheorie een spel waarbij de winst voor de één verlies is voor de ander. De totale opbrengst blijft constant. Dodgson was in de 19e eeuw de enige die fundamentele kwesties inzake speltheorie, in zijn geval stemtheorie, te berde bracht. Pas in 1928 publiceerde John von Neumann[10] een eerste formeel systematisch spel-theoretisch bijdrage in de vorm van de minimax-stelling, die de volledige strategie beschrijft van spelers in tweepersoons nulsomspellen.
Niemand/Niets
In zijn boek “Euclid and his Modern Rivals” introduceerde Carroll een zekere Herr Niemand. Dit is de fantasienaam van een Duitse professor die “alle boeken heeft gelezen en klaar staat om elke bewering waar of niet-waar te verdedigen”. In dit fragment gaat het om het toekennen van de naam Niemand aan een persoon. Wellicht heeft dit ook te maken met een verwijzing naar de lege verzameling. Het eerste optreden van een zekere Nobody is bij de theevisite als Alice tegen de Maartse Haas zegt: “Nobody asked your opinion”.
De lege verzameling is een belangrijke wiskundige entiteit binnen de verzamelingentheorie. Niets is niet niets maar iets belangrijks. Carroll was pionier door in te zien dat niets een bestaande reële entiteit is. Een goed voorbeeld hiervan is de scène in hoofdstuk 8 van Wonderland als alleen de kop van de Cheshire Kat zichtbaar is en er sprake is van een dispuut tussen de Hartenkoning, de Hartenkoningin en de beul over het onthoofden van een kop zonder lichaam eraan vast. De beul zegt dat dat niet kan, terwijl de koning beweert dat dat wel kan. Het standpunt van de beul is vrij normaal. Het standpunt van de koning als wiskundige is heel onrealistisch, maar op zich geeft de term onthoofden al aan dat er een hoofd (in dit geval een kop) minimaal aanwezig moet zijn. Anders valt er niets te onthoofden. Aan de minimale en noodzakelijke voorwaarde dat er een kop is wordt dus voldaan. Ook aan de mogelijke tweedeling bij het afsnijden wordt voldaan omdat er twee elementen zijn volgens de wiskundige koning, namelijk het hoofd en het niet iets. Cantor[11] kwam in 1874 met zijn eerste theoretisch werk over het wiskundige begrip verzamelingen.



Datum
In Wonderland zijn 3 kalenderdagen van belang:
- 4 – 7 – 1862, de datum van het bekende boottochtje. Alice was toen 10 jaar oud.
- 4 mei, de verjaardag van Alice die in het boek 7 jaar oud is.
- 14 maart, de dag dat de Maartse Haas gek werd. Dat is niet verwonderlijk, omdat 14 maart (geschreven als 3, 14) pi-dag (π-dag) is.[12]

Leeftijden
In Spiegelland is Alice 7½jaar oud. De leeftijd van de Witte Koningin is 101 jaar, 5 maanden en 1 dag. Dat zijn omgerekend 37.044 dagen inclusief wat schrikkeldagen. Samen met de Rode Koningin zijn dat 74.088 dagen en hoe vreemd (?) ook, 74088 = 423. Tenslotte staan beide koninginnen en Alice (3 koninginnen) op hetzelfde schaakbord. En natuurlijk is 7½ al een exact getal! Dat “exactually” is voor wiskundigen een dom pleonasme.


Voetnoten
[1] Een caucus is een term voor een comité van politieke lobbyisten die een competitieve strijd tussen kandidaten tracht te vermijden door vooraf afspraken te gaan maken of door het promoten van een enkele kandidaat.
[2] https://www.hhofstede.nl/paradoxen/achilles.htm. “What the Tortoise Said to Achilles” verscheen in het tijdschrift Mind van april 1895 waarin Lewis Carroll 2 problemen presenteerde die logici onder ogen moeten zien bij het vaststellen van gevolgtrekkingen bij bewijzen.
[3] Zie voor enige achtergrond over modulair rekenen: https://nl.wikipedia.org/wiki/Modulair_rekenen.
[4] Pierre de Fermat (1607-1665), van origine een Franse jurist, werd beroemd door zijn zogeheten grote stelling van Fermat waarin hij het vermoeden uitte dat de vergelijking an + bn = cn geen oplossing(en) heeft voor n groter dan 2 met a, b, c en n positieve gehele getallen. Pas na ruim 3 eeuwen bewees de Britse wiskundige Andrew Wiles (1953) in 1994 dit vermoeden. Voor n=2 zijn er oneindig veel getallen a, b en c die aan de vergelijking a2 + b2 = c2 voldoen, bijvoorbeeld: de combinatie 3, 4 en 5 met al hun veelvouden; ook de combinatie 5, 12 en 13 en alle veelvouden daarvan voldoen.
[5] Aan de hand van de kleine stelling van Fermat kun je eigenschappen van vaak zeer grote getallen afleiden, zonder dat je die grote getallen zelf berekent.
[6] Een irrationaal getal is een reëel getal dat niet geschreven kan worden als deling van 2 gehele getallen. Is een reëel getal wel te schrijven als een deling van 2 gehele getallen dan is dat een rationaal getal. De verzameling van reële getallen bestaat uit de verzameling rationale getallen en de verzameling irrationale getallen. Voorbeelden van irrationale getallen zijn √2, π en 3√42 . De ‘meeste’ reële getallen zijn irrationaal.
[7] Meestal wordt tulips-roots in het Nederlands vertaald met tulpenbollen. Mathematisch zou een betere Nederlandse vertaling zijn: een bosje wortelen.
[8] Bij de rechtzaak worden ook 2 guinea-pigs (cavia’s) afgevoerd. Een guinea is een oude Engelse munteenheid van 21 shilling. En 2 x 21 = …!
[9] Spoed is de verplaatsing langs de as per omwenteling. Een spiraal is een 3-dimensionale kromme die rond een bepaald punt draait en steeds dichter dit punt nadert of zich er steeds verder van verwijdert.
[10] John von Neumann (1903-1957) was in tegenstelling tot de meeste wiskundigen een zeer extravagante persoonlijkheid. Hij was een geniale wiskundige en heeft op veel deelgebieden binnen de wiskunde belangrijke bijdragen geleverd. Hij wordt beschouwd als de grondlegger van de speltheorie. Zie ook: https://nl.wikipedia.org/wiki/John_von_Neumann
[11] Georg Cantor (1845-1918) was een Duitse wiskundige die het wiskundige begrip oneindigheid formaliseerde en verdiepte. Hij bewees in 1874 dat de oneindige verzameling reële getallen “talrijker” is dan de oneindige verzameling natuurlijke getallen, waardoor hij aantoonde dat er oneindige verzamelingen zijn van verschillende “grootte”. Het artikel hierover markeerde het begin van zijn theorie over verzamelingen. Zijn werk is ook van filosofisch belang.
[12] Zoals zoveel wiskundigen had Carroll een fascinatie voor het irrationale (niet-rationale) getal π . Op 21 maart 1878 schreef hij in zijn dagboek dat hij zinnen in versvorm had geschreven waarmee hij π in 102 decimalen kon benaderen. Het aantal letters in een woord van het vers vertegenwoordigt daarbij het desbetreffende cijfer in de decimalen van π . Ook noteerde hij dat hij in staat was π π in 4 decimalen nauwkeurig uit te rekenen. In 14 minuten! Lange tijd werd Dodgson door mensen lastiggevallen die meenden de kwadratuur van een cirkel te hebben opgelost of “bewijzen” leverden dat π toch echt wel een rationaal getal was. De kwadratuur van een cirkel is de vraag of het mogelijk is om, met behulp van alleen passer en liniaal in een eindig aantal stappen een vierkant te construeren met exact dezelfde oppervlakte als een gegeven cirkel. In 1882 bewees de Duitse wiskundige Ferdinand Lindemann (1852-1938) op een afdoende manier dat de kwadratuur van een cirkel onmogelijk is. Dodgson was niet op de hoogte van dit bewijs. In 1865 publiceerde Dodgson het pamflet “The New Method of Evaluation as Applied to π”. Dit pamflet van 4 pagina’s is een anonieme parodie en een humorvolle bijdrage aan de controverse over het salaris van Benjamin Jowett als professor Grieks, waarbij gebruik wordt gemaakt van 5 vindingrijke pseudo-algebraïsche methoden om π en dus het salaris van Jowett te benaderen.
[print_button]


